| Autor | Beitrag | ||||||
|---|---|---|---|---|---|---|---|
Dude566       
Beiträge: 1592 Erhaltene Danke: 79 W8, W7 (Chrome, FF, IE) Delphi XE2 Pro, Eclipse Juno, VS2012 |
Ich verstehe die Zusammenhänge zwischen der normalen Funktion und ihren Ableitungen nicht, z.B. wie man die Hoch- und Tiefpunkte dadurch herausfindet.
Habe dort mal schnell drüber geschaut doch es nicht wirklich verstanden, so das ich es mir auch behalten kann. www.mathe-cd.de/4_Fu...a%20KDisk1%20SOD.pdf Kann mir hier einer vll kurz und bündig die Zusammenhänge aufzählen? Gruß Dude566 _________________ Es gibt 10 Gruppen von Menschen: diejenigen, die das Binärsystem verstehen, und die anderen. |
||||||
AXMD       
Beiträge: 4006 Erhaltene Danke: 7 Windows 10 64 bit C# (Visual Studio 2019 Express) |
Die erste Ableitung gibt die Steigung an, anschaulich wird das z.B. anhand einer Weg-Zeit-Funktion. Wenn die Funktion s=f(t) den zurückgelegten Weg s in Abhängigkeit der Zeit t angibt, dann ist die erste Ableitung v=f'(t) die Geschwindigkeit. Dort, wo die Geschwindigkeit 0 ist ("Auto steht"), ist ein Hoch- bzw. Tiefpunkt.
AXMD Zuletzt bearbeitet von AXMD am Sa 09.05.09 16:55, insgesamt 1-mal bearbeitet |
||||||
Dude566         
Beiträge: 1592 Erhaltene Danke: 79 W8, W7 (Chrome, FF, IE) Delphi XE2 Pro, Eclipse Juno, VS2012 |
Ja das heist doch ich muss um die X-Koordinate herauszufinden die 1. Ableitung = 0 setzen. Die Werte ich dann bekomme in die normale Funktion einsetzen und ich bekomme die passenden Y-Werte.
Ich habe einen TI Voyage200 mit dem ich das berechnen soll, wie folgen denn dort die Eingaben. 2.) Was ist denn jetzt eigentlich der Unterschied zwischen einem Wende- und einem Sattelpunkt? Also beim Sattelpunkt gibt es keine waagerechte Tangente und die Steigung ändert sich nicht oder? Wie kann ich diese beiden berechnen? Gruß Dude566 _________________ Es gibt 10 Gruppen von Menschen: diejenigen, die das Binärsystem verstehen, und die anderen. |
||||||
AXMD       
Beiträge: 4006 Erhaltene Danke: 7 Windows 10 64 bit C# (Visual Studio 2019 Express) |
Richtig, das sind dann die entsprechenden X-Koordinaten, an denen die Steigung 0 ist
Ich hatte diesen TI auch und wenn ich mich richtig erinnere gibt es sogar eine eingebaute Funktion dafür
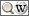 WENDEPUNKT WENDEPUNKT 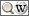 SATTELPUNKT SATTELPUNKT AXMD |
||||||
tommie-lie       
Beiträge: 4373 Ubuntu 7.10 "Gutsy Gibbon" |
solve(∂(f(x),x)=0,x) und für f(x) die Funktion einsetzen, für die man es betimmen soll. _________________ Your computer is designed to become slower and more unreliable over time, so you have to upgrade. But if you'd like some false hope, I can tell you how to defragment your disk. - Dilbert |
||||||
Dude566         
Beiträge: 1592 Erhaltene Danke: 79 W8, W7 (Chrome, FF, IE) Delphi XE2 Pro, Eclipse Juno, VS2012 |
Und dann einfach die Werte einsetzen... so oder? z.B.: f(4.40161) und dann bekomme ich die passenden Y-Werte dazu und kann die Extremstellen aufzeigen. _________________ Es gibt 10 Gruppen von Menschen: diejenigen, die das Binärsystem verstehen, und die anderen. |
||||||
tommie-lie       
Beiträge: 4373 Ubuntu 7.10 "Gutsy Gibbon" |
Er liefert dir dann alle Werte für x, die die Bedingung erfüllen. Ist nach den Extremstellen gefragt, reicht das, ist nach den Extrempunkten gefragt, musst du natürlich noch den Funktionswert an der/den Stelle(n) ausrechnen. Denk darüber nach und überlege selbst ob dein Vorschlag richtig ist, oder nicht
_________________ Your computer is designed to become slower and more unreliable over time, so you have to upgrade. But if you'd like some false hope, I can tell you how to defragment your disk. - Dilbert |
||||||
Dude566         
Beiträge: 1592 Erhaltene Danke: 79 W8, W7 (Chrome, FF, IE) Delphi XE2 Pro, Eclipse Juno, VS2012 |
Wieso sollte er es nicht sein, wenn ich in eine Funktion die x-Werte eingebe liefert er mir doch die zugehörigen Y-Werte.
Oder was soll daran falsch sein? 2.)Gegeben ist f durch eine Gleichung f(x)=x^3-6x^2+8x+2 a) In welchen Bereichen hat der Graph zu f eine Links- bzw. eine Rechtskurve? Wie soll ich denn die Bereiche herausfinden, ich weis das wenn in der 3.Ableitung der Wert größer 0 ist, dann macht er eine Rechtskurve und andersrum. _________________ Es gibt 10 Gruppen von Menschen: diejenigen, die das Binärsystem verstehen, und die anderen. |
||||||
tommie-lie       
Beiträge: 4373 Ubuntu 7.10 "Gutsy Gibbon" |
Dir scheinen nur die Grundlagen zu fehlen, deswegen solltest du lieber mal selber drüber nachdenken, dann behältst du es besser, insbesondere wenn du dich gerade für eine Prüfung vorbereitest.
_________________ Your computer is designed to become slower and more unreliable over time, so you have to upgrade. But if you'd like some false hope, I can tell you how to defragment your disk. - Dilbert |
||||||
Dude566         
Beiträge: 1592 Erhaltene Danke: 79 W8, W7 (Chrome, FF, IE) Delphi XE2 Pro, Eclipse Juno, VS2012 |
Puuh, das muss ich mir erst nochmal durchlesen und drüber nachdenken.
Aber danke schonmal. _________________ Es gibt 10 Gruppen von Menschen: diejenigen, die das Binärsystem verstehen, und die anderen. |
||||||
Dude566         
Beiträge: 1592 Erhaltene Danke: 79 W8, W7 (Chrome, FF, IE) Delphi XE2 Pro, Eclipse Juno, VS2012 |
Also wenn jede der 3 Ableitungen = 0 ist dann ist es ein Sattelpunkt.
Und bei einer Wendestelle muss man die 2. gleich Null setzten und den Wert dann in die 3. Ableitung einsetzten. Kommt dann ein Wert größer Null heraus ist es eine Rechtskurve. Stimmt doch so oder? _________________ Es gibt 10 Gruppen von Menschen: diejenigen, die das Binärsystem verstehen, und die anderen. |
||||||
jfheins       
Beiträge: 918 Erhaltene Danke: 158 Win 10 VS 2013, VS2015 |
Nein.
Ein Sattelpunkt ist es, wenn die erste und die zweite Ableitung gleich null ist. Beispiel: y(x) := x^4-2*x^3+2*x-1 Bei x=1 ist ein Sattelpunkt - 1. und 2. Ableitung sind gleich null, die 3. Ableitung ist 12 Bei x = -0.5 ist die erste Ableitung 0 aber die zweite ist 9 - also ein Minimum. Mal ne kleine Tabelle (oben 1. Ableitung, links 2. Ableitung)
|
||||||
tommie-lie       
Beiträge: 4373 Ubuntu 7.10 "Gutsy Gibbon" |
Deine Annahme, daß das Vorzeichen der dritten Ableitung angibt, ob es eine Links- oder Rechtskurve ist, war bereits falsch, ist mir zu spät aufgefallen. Die Aussage stimmt natürlich für die zweite Ableitung, nicht für die dritte. Dein Ansatz, die Wendepunkte zu bestimmen, ist natürlich richtig, denn die Wendepunkte überführen eine Links- in eine Rechtskurve. Allerdings bekommst du damit lediglich Intervalle. Angenommen dein Polynom hat in der zweiten Ableitung Nullstellen (=Wendepunkte) bei x=5 und x=9. Dann hast du drei Intervalle: (-unendlich, 5), (5, 9) und (9, +unendlich). An den Stellen 5 und 9 hast du gar keine Krümmung. Um dann noch herauszufinden, ob es sich in den Intervallen um eine Links- oder Rechtskurve handelt, musst du jeweils aus einem Intervall eine Zahl wählen und sie in die zweite Ableitung einsetzen. Das kann natürlich nicht die 5 oder die 9 sein, denn dort herrscht ja keine Krümmung. Also nimmst du Beispielsweise die drei Zahlen 4, 7 und 12. Wenn du dir das Leben einfacher machen willst, und du alle Wendepunkte bestimmt hast, reicht es auch, die Krümmung in nur einem einzigen Intervall zu bestimmen. Die direkten Nachbarintervalle haben dann einen umgekehrten Krümmungssinn, die übernächsten wieder den gleichen und so weiter. Grund: An jedem Wendepunkt ändert sich eine Links- in eine Rechtskurve und umgekehrt. Weißt du, daß du von einer Linkskurve kommst und überschreitest einen Wendepunkt, dann bist du anschließend in einer Rechtskurve und umgekehrt. Die Idee, auf die ich dich eigentlich führen wollte: Du kennst von einer Funktion (unabhängig davon, ob es jetzt eine Ableitung ist und die wievielte es ist) folgende Eigenschaften: Ist ihr Wert kleiner 0, dann Ereignis A, ist ihr Wert größer 0, dann Ereignis B. Wenn du jetzt die Bereiche bestimmen sollst, in denen A oder B eintreten, musst du die Nullpunkte dieser Funktion bestimmen, indem du sie gleichsetzt. Immer dann, wenn es einen Wechsel von Ereignis A zu Ereignis B gibt, gibt es einen Nulldurchgang, weil das Vorzeichen ja wechseln muss. Durch Bestimmen der Nullstellen hast du also den ersten Teil der Aufgabe gelöst, nämlich die Bereihe einzugrenzen. Dann musst du nur noch bestimmen, ob innerhalb eines Bereiches nun A oder B gilt. Wenn c1 und c2 die Grenzen eines solchen Bereiches sind, kriegst du mit (c1+c2)/2 die Mitte des Bereiches, wenn du die Funktion dort auswertest, weißt du, ob zwischen c1 und c2 Ereignis A oder Ereignis B eintritt.
_________________ Your computer is designed to become slower and more unreliable over time, so you have to upgrade. But if you'd like some false hope, I can tell you how to defragment your disk. - Dilbert |
||||||
Dude566         
Beiträge: 1592 Erhaltene Danke: 79 W8, W7 (Chrome, FF, IE) Delphi XE2 Pro, Eclipse Juno, VS2012 |
Also die typische Befehlsfolge um Wendestellen herauszufinden wäre doch dann:
a*x^3+b*x^2-c+x+d -> f(x) d(f(x),x) -> f1(x) d(f1(x),x) -> f2(x) solve.... Wie muss ich dann weiter vorgehen mit meinem TI, stehe gerade auf dem Schlauch? _________________ Es gibt 10 Gruppen von Menschen: diejenigen, die das Binärsystem verstehen, und die anderen. |
||||||
Jakob_Ullmann       
Beiträge: 1747 Erhaltene Danke: 15 Win 7, *Ubuntu GNU/Linux* *Anjuta* (C, C++, Python), Geany (Vala), Lazarus (Pascal), Eclipse (Java) |
Tja, also du könntest es verschachteln. Ich hab mir dafür mal eine Funktion programmiert.
|
||||||
Dude566         
Beiträge: 1592 Erhaltene Danke: 79 W8, W7 (Chrome, FF, IE) Delphi XE2 Pro, Eclipse Juno, VS2012 |
x^3-6*x^2+8*x+2 -> f(x)
d(f(x),x) -> f1(x) d(f1(x),x) -> f2(x) d(f2(x),x) -> f3(x) zeros(f2(x),x) Die Werte dann in die 3. Ableitung zum Prüfen einsetzten, und wenn sie ungleich null sind, sind es auch Wendestellen. Da kommt dann bei mir für die das obige Polynom der Wendepunkt (2/2) heraus. Richtig? Die Werte dann in die normal Form einsetzten und ich bekomme die passenden Y-Werte und kann die Punkte der Wendestellen angeben. Is doch richtig so oder? Wie kann man sich dafür ne Funktion schreiben? Das wäre ja echt super für die Arbeit, merkt der Lehrer eh net. ^^ _________________ Es gibt 10 Gruppen von Menschen: diejenigen, die das Binärsystem verstehen, und die anderen. |
||||||
Jakob_Ullmann       
Beiträge: 1747 Erhaltene Danke: 15 Win 7, *Ubuntu GNU/Linux* *Anjuta* (C, C++, Python), Geany (Vala), Lazarus (Pascal), Eclipse (Java) |
Als Einstieg: Das TI-89 Titanium / Voyage 200 Handbuch nehmen und bei "Vorschau" gucken. Der Rest sollte klar gehen. Du nimmst dafür das Menü Prgm (Program Editor). Du nimmst 3:New... Stellst bei Type 2:Function statt 1:Program ein und schreibst. Als Einleitung hier auch mal mein Source einer einfachen Funktion (1-zeilig, erspart mir aber trotzdem ne Menge Arbeit):
oder:
Aufruf dann im Menü Home: für alle lokalen Maxima von f(x)=x³-5x Schade nur, dass wir in der Schule einen numerischen von CASIO nehmen müssen, da geht das logischerweise nicht (u. a. auch, da der nur "richtige" Programme, keine Funktionen, unterstützt). Nicht wirklich gut, aber ein Anfang: de.wikibooks.org/wiki/TI-Basic edit: Deine Wendepunktberechnung ist aber noch nicht vollständig:
Zumindest, falls du es via Funktion automatisieren willst, solltest du das beachten (and ist hier die Schnittmenge, oder eben einfach AND). edit2: das != bedeutet übrigens ungleich, erreichbar über 2ND - V. |
||||||
Dude566         
Beiträge: 1592 Erhaltene Danke: 79 W8, W7 (Chrome, FF, IE) Delphi XE2 Pro, Eclipse Juno, VS2012 |
Wieso, ich habe doch zeros verwendet damit bekomme ich doch die Nullstellen der 2. Ableitung, und die brauche ich ja schließlich.
PS: Handbuch habe ich für den Rechner nicht, er gehört der Schule. _________________ Es gibt 10 Gruppen von Menschen: diejenigen, die das Binärsystem verstehen, und die anderen. |
||||||
Jakob_Ullmann       
Beiträge: 1747 Erhaltene Danke: 15 Win 7, *Ubuntu GNU/Linux* *Anjuta* (C, C++, Python), Geany (Vala), Lazarus (Pascal), Eclipse (Java) |
Das ist natürlich schlecht, dass der Taschenrechner der Schule gehört... Aber das sollte auch kein Problem sein, nach Lesen dieser Einleitung und ein bisschen klicken im Menü sollte das Programmieren in TI-Basic eigentlich mehr oder weniger intuitiv gehen.
Du hast zwar die Nullstellen der zweiten Ableitung, jedoch muss, damit es ein Wendepunkt ist, die dritte Ableitung an dieser Stelle ungleich null sein. Und wenn du das schon automatisierst, kannst du das den Taschenrechner eigentlich gleich mit machen lassen. |
||||||
Dude566         
Beiträge: 1592 Erhaltene Danke: 79 W8, W7 (Chrome, FF, IE) Delphi XE2 Pro, Eclipse Juno, VS2012 |
ja ich kann aber doch die Werte die ich nach dem zeros bekomme auch einfach in die 3. Ableitung einsetzen und dann bekomme ich doch die Punkte. Dauert zwar länger aber so verstehe ich das Prinzip besser. So gehts doch auch oder?
_________________ Es gibt 10 Gruppen von Menschen: diejenigen, die das Binärsystem verstehen, und die anderen. |
||||||

















